Momentum dan Impuls

A. Momentum dan Impuls

1. Momentum

Sebuah truk bermuatan penuh akan lebih sulit untuk berhenti daripada sebuah mobil kecil, walaupun kecepatan kedua kendaraan itu sama. Kenapa demikian? Dalam pengertian fisisnya dikatakan bahwa momentum truk lebih besar daripada mobil. Secara Fisika, pengertian momentum adalah hasil kali antara massa benda (m) dan kecepatannya (v), yang dituliskan sebagai berikut.

p = m x v                       (1-1)

dengan:

m = massa benda (kg),

v = kecepatan benda (m/s), dan

p = momentum benda (kgm/s).

Gambar 1. Mobil bermassa m, bergerak dengan kecepatan v. Momentumnya p = m x v.

Dari Persamaan (1–1) tersebut, dapat dilihat bahwa momentum merupakan besaran vektor karena memiliki besar dan arah.

Contoh Soal 1 :

Sebuah mobil bermassa 1.500 kg bergerak dengan kecepatan 36 km/jam. Berapakah momentum mobil tersebut?

Kunci Jawaban :

Diketahui: m = 1.500 kg dan v = 36 km/jam.

m = 1.500 kg

v = 36 km/jam = 10 m/s

Momentum mobil: p = mv = (1.500 kg)(10 m/s) = 15.000 kgm/s.

Contoh Soal 2 :

Perhatikan data berikut ini.

a. Mobil bermassa 2.000 kg yang berisi seorang penumpang bergerak dengan kecepatan 72 km/jam.

b. Seseorang mengendarai motor bermassa 100 kg dengan kecepatan 108 km/jam.

c. Seseorang naik motor bermassa 100 kg dan membonceng seorang lainnya, bergerak dengan kecepatan 54 km/jam.

Jika massa orang 50 kg, data manakah yang memiliki momentum terbesar?

Kunci Jawaban :

Diketahui : m_mobil = 2.000 kg, m_motor = 100 kg, v_{motor ke–2} = 54 km/jam = 15 m/s,

v_{motor ke–1} = 108 km/jam = 30 m/s, dan v_mobil =72 km/jam = 20 m/s

a. Momentum mobil dengan seorang penumpang:

p_mobil = (m_orang + m_mobil)(v_mobil)

p_mobil = (50 kg + 2.000 kg)(20 m/s) = 41.000 kgm/s

b. Momentum motor dengan seorang pengendara:

p_motor = (mo_rang + m_motor)(v_{motor ke–1})

p_motor = (50 kg + 100 kg)(30 m/s) = 4.500 kgm/s

Jadi, momentum yang terbesar adalah momentum yang dimiliki oleh motor dengan seorang pengendara, yaitu 4.500 kgm/s.

Contoh Soal 3 :

Benda A dan benda B masing-masing bermassa 2 kg dan 3 kg, bergerak saling tegak lurus dengan kecepatan masing-masing sebesar 8 m/s dan 4 m/s. Berapakah momentum total kedua benda tersebut?

Kunci Jawaban :

Diketahui: mA = m_A = 2 kg, m_B = 3 kg, v_A = 8 m/s, dan v_B = 4 m/s.

p_A = m_Av_A = (2 kg)(8 m/s) = 16 kgm/s

p_B = m_Bv_B = (3 kg)(4 m/s) = 12 kgm/s

Momentum adalah besaran vektor sehingga untuk menghitung besar momentum total kedua benda, digunakan penjumlahan vektor:

p_total = (pA₂ + pB₂)^1/2 = [(16 kgm/s)² + (12 kgm/s)²]^1/2 = 20 kgm/s.

2. Impuls

Cobalah Anda tendang sebuah bola yang sedang diam. Walaupun kontak antara kaki Anda dan bola hanya sesaat, namun bola dapat bergerak dengan kecepatan tertentu. Dalam pengertian momentum, dikatakan bahwa pada bola terjadi perubahan momentum akibat adanya gaya yang diberikan dalam selang waktu tertentu. Gaya seperti ini, yang hanya bekerja dalam selang waktu yang sangat singkat, disebut gaya impulsif.

Gambar 2. Gaya yang diberikan pada bola tenis hanya bekerja dalam selang waktu singkat. Gaya ini menyebabkan bola tenis bergerak dengan kecepatan dan lintasan tertentu. [2]

Oleh karena itu, perkalian antara gaya dan selang waktu gaya itu bekerja pada benda disebut impuls. Secara matematis, dituliskan sebagai

I = F Δt (5–2)              (1–2)

Besarnya impuls dapat dihitung dengan menggunakan grafik hubungan gaya F terhadap waktu t (grafik F – t). Perhatikan Gambar 3. berikut.

Gambar 3. Luas daerah di bawah grafik F – t menunjukkan impuls yang dialami benda.

Gaya impulsif yang bekerja pada benda berada pada nilai nol saat t₁  Kemudian, gaya tersebut bergerak ke nilai maksimum dan akhirnya turun kembali dengan cepat ke nilai nol pada saat t₂  Oleh karena luas daerah di bawah kurva gaya impulsif sama dengan luas persegipanjang gaya rata-rata ( F )yang bekerja pada benda, grafik hubungan antara F dan t dapat digambarkan sebagai besar impuls yang terjadi pada benda.

Jika gaya yang diberikan pada benda merupakan suatu fungsi linear, impuls yang dialami oleh benda sama dengan luas daerah di bawah kurva fungsi gaya terhadap waktu, seperti terlihat pada Gambar 4.

Gambar 4. Impuls = luas daerah yang diarsir.

Dengan memerhatikan Persamaan (1–2), Anda dapat menyimpulkan bahwa gaya dan selang waktu berbanding terbalik. Perhatikan Tabel 1. berikut.

Tabel 1. Kombinasi antara Gaya dan Waktu yang Dibutuhkan untuk Menghasilkan Impuls Sebesar 100 Ns

Gaya (N)	Waktu (s)	Impuls (Ns)
100	1	100
50	2	100
25	4	100
10	10	100
4	25	100
2	50	100
1	100	100
0,1	1.000	100

Besarnya impuls yang dibentuk adalah sebesar 100 Ns, namun besar gaya dan selang waktu gaya tersebut bekerja pada benda bervariasi. dari Tabel 1. tersebut, dapat dilihat bahwa jika waktu terjadinya tumbukan semakin besar (lama), gaya yang bekerja pada benda akan semakin kecil. oleh karena itu, dapat disimpulkan bahwa waktu kontak antara gaya dan benda sangat memengaruhi besar gaya yang bekerja pada benda saat terjadi tumbukan.

Catatan Fisika :

Pesawat Luar Angkasa

Peluncuran Pesawat Luar Angkasa AS, Columbia. [3]

Pesawat luar angkasa yang akan bergerak menuju orbit harus mendapatkan momentum yang sangat besar agar kecepatannya bisa mengatasi percepatan gravitasi Bumi. Oleh karena itu, mesin pesawat harus mampu mengeluarkan gaya dorong yang sangat besar (sekitar 30 × 10⁶ N). (Sumber: Jendela Iptek, 1997)

3. Hubungan antara Impuls dan Perubahan Momentum

Pada pelajaran sebelumnya, telah Anda ketahui bahwa jika pada sebuah benda bermassa m, bekerja sebuah gaya F yang besarnya tetap selama t sekon, pada benda itu berlaku persamaan

v_t = v₀ + aΔt

dengan a = F/m (Hukum II Newton) sehingga v_t = v₀ + (F/m) Δt

v_t = v₀ + (F/m) Δt

sehingga :

FΔt = m(v_t – v₀)                                       (1–3)

dengan: 

mv₀ = momentum awal, dan

mv_t = momentum akhir.

Oleh karena FΔt = impuls dari gaya F, Persamaan (1–3) dapat diartikan bahwa impuls suatu benda sama dengan perubahan momentum yang dialami benda tersebut. Secara matematis dituliskan sebagai :

I = Δp                                                     (1–4)

Contoh Soal 4 :

Sebuah benda yang massanya 0,5 kg berada dalam keadaan diam. Kemudian, benda tersebut dipukul dengan gaya sebesar F sehingga benda bergerak dengan kecepatan 10 m/s. Jika pemukul menyentuh benda selama 0,01 sekon, tentukanlah:

a. perubahan momentum benda, dan

b. besarnya gaya F yang bekerja pada benda.

Kunci Jawaban :

Diketahui: m = 0,5 kg, v = 10 m/s, dan Δt = 0,01 s.

a. Perubahan momentum ( Δp):

Δp = mv – mv₀ = (0,5 kg)(10 m/s) – (0,5 kg)(0 m/s) = 5 Ns

b. Besarnya gaya F:

F Δt = mv – mv₀

F(0,01 s) = 5 Ns → F = (5 Ns / 0,01 s) = 500 newton.

Contoh Soal 5 :

Sebuah benda bermassa 2 kg berada dalam keadaan diam di permukaan meja yang licin. Kemudian, benda itu digerakkan secara mendatar oleh sebuah gaya mendatar F. Gaya tersebut berubah terhadap waktu menurut F = 30 – 6t, dengan t dalam s dan F dalam N. Tentukanlah:

a. grafik hubungan gaya (F) terhadap waktu (t),

b. impuls yang bekerja pada benda tersebut, dan

c. kecepatan benda setelah 5 sekon.

Kunci Jawaban :

Diketahui: m = 2 kg dan F = 30 – 6t.

a. Grafik hubungan gaya (F) terhadap waktu (t) dari persamaan F = 30 – 6t adalah sebagai berikut.

b. Impuls = luas daerah di bawah kurva

Impuls = luas segitiga

Impuls = 1/2 (5 s)(30 N) = 75 Ns

c. Kecepatan benda setelah 5 sekon ditentukan dengan persamaan berikut.

Impuls = perubahan momentum

F Δt = mv – mv₀

75 Ns = (2 kg)(v) – (2 kg)(0 m/s)

v = 37,5 m/s

Catatan Fisika :

Ayunan balistik digunakan untuk mengukur kecepatan peluru dengan cara menembakkan peluru bermassa m ke balok kayu yang tergantung bebas bermassa m. Apabila simpangan ayunan diukur, akan didapatkan momentum tumbukan antara peluru dan balok kayu sehingga kecepatan peluru dapat diukur.

B. Hukum Kekekalan Momentum

1. Hukum Kekekalan Momentum

Dua benda dapat saling bertumbukan, jika kedua benda bermassa m₁ dan m₂ tersebut bergerak berlawanan arah dengan kecepatan masing-masing v₁ dan v₂  Apabila sistem yang mengalami tumbukan itu tidak mendapatkan gaya luar, menurut Persamaan (1–4) diketahui bahwa apabila F = 0 maka Δp = 0 atau p = konstan. Dengan demikian, didapatkan bahwa jumlah momentum benda sebelum tumbukan akan sama dengan jumlah momentum benda setelah tumbukan. Hal ini disebut sebagai Hukum Kekekalan Momentum. 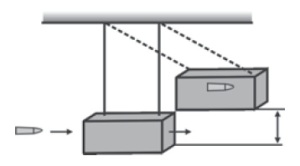Perhatikanlah Gambar 5.

Gambar 5. Urutan gerak dua benda bermassa m1 dan m2 mulai dari sebelum tumbukan hingga sesudah tumbukan.

Sebelum tumbukan, kecepatan masing-masing adalah benda v₁ dan v₂. Sesudah tumbukan, kecepatannya menjadi v₁' dan v₂'. Apabila F₁₂ adalah gaya dari m₁ yang dipakai untuk menumbuk m₂, dan F₂₁ adalah gaya dari m₂ yang dipakai untuk menumbuk m₁ maka menurut Hukum III Newton diperoleh hubungan sebagai berikut:

F(_aksi) = –F(_reaksi) atau F₁₂ = –F₂₁. Jika kedua ruas persamaan dikalikan dengan selang waktu Δt maka selama tumbukan akan didapatkan:

F₁₂Δt = –F₂₁Δt

Impuls ke-1 = –Impuls ke-2

(m₁v₁ – m₁v₁')= – (m₂v₂ – m₂v₂')

m₁v₁ – m₁v₁' = – m₂v₂ + m₂v₂' .... (a)

Apabila Persamaan (a) dikelompokkan berdasarkan kecepatannya, persamaan tersebut dapat dituliskan sebagai berikut.

m₁v₁ – m₁v₁' = – m₂v₂ + m₂v₂'                            (1–5)

Contoh Soal 6 :

Dua benda masing-masing bermassa m, bergerak berlawanan arah dengan kecepatan masing-masing 20 m/s dan 15 m/s. Setelah tumbukan, kedua benda tersebut bersatu. Tentukanlah kecepatan kedua benda dan arah geraknya setelah tumbukan.

Kunci Jawaban :

Diketahui: m₁ = m₂ = m, v₁ = 20 m/s, dan v² = 15 m/s.

v₂ bertanda negatif karena geraknya berlawanan arah dengan arah gerak benda pertama. Oleh karena setelah tumbukan kedua benda bersatu dan bergerak bersamaan maka kecepatan kedua benda setelah tumbukan adalah v₁' = v₂' = v'

sehingga :

m₁v₁ + m₂v₂ = (m₁ + m₂)v'

m(20 m/s) + m(–15 m/s) = (m + m)v'

Jadi, kecepatan kedua benda 2,5 m/s, searah dengan arah gerak benda pertama (positif).

Contoh Soal 7 :

Seorang penumpang naik perahu yang bergerak dengan kecepatan 4 m/s. Massa perahu dan orang itu masing-masing 200 kg dan 50 kg. Pada suatu saat, orang tersebut meloncat dari perahu dengan kecepatan 8 m/s searah gerak perahu. Tentukanlah kecepatan perahu sesaat setelah orang tersebut meloncat.

Kunci Jawaban :

Diketahui: m_p = 200 kg, m₀ = 50 kg, dan v₀ = 8 m/s.

(m_p + m₀)v = m_pv_p' + m₀v₀'

(200 kg + 50 kg) (4 m/s) = (200 kg)v_p' + (50 kg)(8 m/s)

1.000 kgm/s = (200 kg) v_p' + 400 kgm/s

600 kgm/s = (200 kg) v_p'

v_p' = 3 m/s

Contoh Soal 8 :

Seseorang yang massanya 45 kg membawa senapan bermassa 5 kg. Dalam senapan tersebut, terdapat sebutir peluru seberat 0,05 kg. Diketahui orang tersebut berdiri pada lantai yang licin. Pada saat peluru ditembakkan dengan kecepatan 100 m/s, orang tersebut terdorong ke belakang. Tentukanlah kecepatan orang tersebut pada saat peluru dilepaskan.

Kunci Jawaban :

Diketahui bahwa Hukum Kekekalan Momentum menyatakan energi mekanik sebelum dan setelah tumbukan adalah sama, dengan m₀ = massa orang = 45 kg, m_s = massa senapan = 5 kg, dan m_p = massa peluru = 0,05 kg, dan v_p = 100 m/s.

(m₀ + m_s + m_p)v = (m₀ + m_s)v₀ + m_pv_p

0 = (45 kg + 5 kg)v₀ + (0,05 kg)(100 m/s)

(–50 kg)v₀ = 5 kgm/s

v₀ = (5 kgm /  − 50 m/s) = –0,1 m/s
Jadi, kecepatan orang tersebut pada saat peluru dilepaskan adalah 0,1 m/s

 jenis jenis tumbukan

Tumbukan yang paling sederhana adalah tumbukan sentral. Tumbukan sentral adalah tumbukan yang terjadi bila titik pusat benda yang satu menuju ke titik pusat benda yang lain. Banyak kejadian dalam kehidupan sehari-hari yang dapat dijelaskan dengan konsep momentum dan impuls. Di antaranya peristiwa tumbukan antara dua kendaraan. Salah satu penggunaan konsep momentum yang penting adalah pada persoalan yang menyangkut tumbukan. Misalnya tumbukan antara partikel-partikel gas dengan dinding tempat gas berada. Hal ini dapat digunakan untuk menjelaskan sifat-sifat gas dengan menggunakan analisis mekanika.

Berdasarkan sifat kelentingan atau elastisitas benda yang bertumbukan, tumbukan dapat dibedakan menjadi tiga, yaitu tumbukan lenting sempurna, tumbukan lenting sebagian, dan tumbukan tidak lenting sama sekali.

Tumbukan Lenting Sempurna

Tumbukan lenting sempurna (elastik) terjadi di antara atom-atom, inti atom, dan partikel-partikel lain yang seukuran dengan atom atau lebih kecil lagi. Dua buah benda dikatakan mengalami tumbukan lenting sempurna jika pada tumbukan itu tidak terjadi kehilangan energi kinetik. Jadi, energi kinetik total kedua benda sebelum dan sesudah tumbukan adalah tetap. Oleh karena itu, pada tumbukan lenting sempurna berlaku hukum kekekalan momentum dan hukum kekekalan energi kinetik. Tumbukan lenting sempurna hanya terjadi pada benda yang bergerak saja.
 

Tumbukan lenting sempurna antara dua benda

Dua buah benda memiliki massa masing-masing m₁ dan m₂ bergerak saling mendekati dengan kecepatan sebesar v₁ dan v₂ sepanjang lintasan yang lurus. Setelah keduanya bertumbukan masing-masing bergerak dengan kecepatan sebesar v’₁ dan v’₂ dengan arah saling berlawanan. Berdasarkan hukum kekekalan momentum dapat ditulis sebagai berikut.

m₁v₁ + m₂v₂ = m₁v’₁ + m₂v’₂

m₁v₁ – m₁v’₁ = m₂v’₂ – m₂v₂

m₁(v₁ – v’₁) = m (v’₂ – v₂)

Sedangkan berdasarkan hukum kekekalan energi kinetik, diperoleh persamaan sebagai berikut.

E_k1 + E_k2 = E’_k1 + E’_k2

½ m₁v₁² + ½ m₂v₂²  = ½ m₁(v₁)² + ½ m₂(v₂)²

m₁((v’₁)² – (v₁)²) = m₂((v’₂)² – (v₂)²)

m₁(v₁ + v’₁)(v₁ – v’₁) = m (v’₂ + v₂)(v’₂ – v₂)

Jika persamaan di atas saling disubtitusikan, maka diperoleh persamaan sebagai berikut.

m₁(v₁ + v’₁)(v₁ – v’₁) = m₁(v’₂ + v₂)(v₁ – v’₁)

v₁ + v’₁ = v’₂ + v₂

v₁ – v₂ = v’₂ – v’₁

-(v₂ – v₁) = v’₂ – v’₁

Persamaan di atas menunjukan bahwa pada tumbukan lenting sempurna kecepatan relatif benda sebelum dan sesudah tumbukan besarnya tetap tetapi arahnya berlawanan.

Tumbukan Tidak Lenting Sama Sekali

etik sehingga hukum kekekalan energi mekanik tidak berlaku. Pada tumbukan jenis ini, kecepatan benda-benda sesudah tumbukan sama besar (benda yang bertumbukan saling melekat). Misalnya, tumbukan antara peluru dengan sebuah target di mana setelah tumbukan peluru mengeram dalam target. Secara matematis dapat ditulis sebagai berikut.

m₁v₁ + m₂v₂ = m₁v’₁ + m₂v’₂

Jika    v’₁ = v’₂ = v’,      maka    m₁v₁ + m₂v₂ = (m₁ + m₂) v’

 Tumbukan tidak lenting sama sekali yang terjadi antara dua benda

Contoh tumbukan tidak lenting sama sekali adalah ayunan balistik. Ayunan balistik merupakan seperangkat alat yang digunakan untuk mengukur benda yang bergerak dengan keceptan cukup besar, misalnya kecepatan peluru. Prinsip kerja ayunan balistik berdasarkan hal-hal berikut.

a. Penerapan sifat tumbukan tidak lenting.

m₁v₁ + m₂v₂ = (m₁ + m₂) v’

m₁v₁ + 0 = (m₁ + m₂) v’

b. Hukum kekekalan energi mekanik

½ (m₁ + m₂)(v’)² = (m₁ + m₂)gh

Jika persamaan pertama disubtitusikan ke dalam persamaan kedua, maka diketahui kecepatan peluru sebelum bersarang dalam balok.

Skema ayunan balistik

Tumbukan Lenting Sebagian

Kebanyakan benda-benda yang ada di alam mengalami tumbukan lenting sebagian, di mana energi kinetik berkurang selama tumbukan. Oleh karena itu, hukum kekekalan energi mekanik tidak berlaku. Besarnya kecepatan relatif juga berkurang dengan suatu faktor tertentu yang disebut koefisien restitusi. Bila koefisien restitusi dinyatakan dengan huruf e, maka derajat berkurangnya kecepatan relatif benda setelah tumbukan dirumuskan sebagai berikut.

Nilai restitusi berkisar antara 0 dan 1 (0  ≤   e  ≤  1 ). Untuk tumbukan lenting sempurna, nilai e = 1. Untuk tumbukan tidak lenting nilai e = 0. Sedangkan untuk tumbukan lenting sebagian mempunyai nilai e antara 0 dan 1 (0 < e < 1). Misalnya, sebuah bola tenis dilepas dari ketinggian h₁ di atas lantai. Setelah menumbuk lantai bola akan terpental setinggi h₂, nilai h₂ selalu lebih kecil dari h₁.

Skema tumbukan lenting sebagian

Coba kita perhatikan gamabr diatas. Kecepatan bola sesaat sebelum tumbukan adalah v1 dan sesaat setelah tumbukan v1 . Berdasarkan persamaan gerak jatuh bebas, besar kecepatan bola memenuhi persamaan :

Untuk kecepatan lantai sebelum dan sesudah tumbukan sama dengan nol (v₂ = v’₂ = 0). Jika arah ke benda diberi harga negatif, maka akan diperoleh persamaan sebagai berikut.

Persamaan diatas digunakan untuk tumbukan lenting sebagian.