BESARAN DAN SATUAN

MATERI BESARAN DAN SATUAN

Pengukuran adalah proses membandingkan nilai besaran yang diukur dengan besaran sejenis yang dipakai sebagai satuan. Hasil dari pada pengukuran merupakan besaran. Besaran adalah suatu yang dapat diukur dan dinyatakan dengan angka dan nilai yang memiliki satuan.
Dari pengertian ini dapat diartikan bahwa sesuatu itu dapat dikatakan sebagai besaran harus mempunyai 3 syarat yaitu
1. dapat diukur atau dihitung
2. dapat dinyatakan dengan angka-angka atau mempunyai nilai
3. mempunyai satuan
Bila ada satu saja dari syarat tersebut diatas tidak dipenuhi maka sesuatu itu tidak dapat dikatakan sebagai besaran.
Besaran berdasarkan cara memperolehnya dapat dikelompokkan menjadi 2 macam yaitu :
1. Besaran Fisika yaitu besaran yang diperoleh dari pengukuran. Karena diperoleh dari pengukuran maka harus ada alat ukurnya. Sebagai contoh adalah massa. Massa merupakan besaran fisika karena massa dapat diukur dengan menggunakan neraca.
2. Besaran non Fisika yaitu besaran yang diperoleh dari penghitungan. Dalam hal ini tidak diperlukan alat ukur tetapi alat hitung sebagai misal kalkulator. Contoh besaran non fisika adalah Jumlah.
Dalam fisika besaran ada dua yaitu besaran pokok dan besaran turunan.
Besaran pokok adalah besaran yang satuannya telah ditetapkan terlebih dahulu dan tidak diturunkan dari besaran lain.
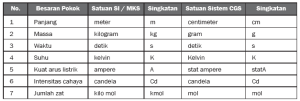
Besaran pokok yang paling umum ada 7 macam yaitu Panjang (m), Massa (kg), Waktu (s), Suhu (K), Kuat Arus Listrik (A), Intensitas Cahaya (cd), dan Jumlah Zat (mol). Besaran pokok mempunyai ciri khusus antara lain diperoleh dari pengukuran langsung, mempunyai satu satuan (tidak satuan ganda), dan ditetapkan terlebih dahulu.

Tabel Besaran Pokok

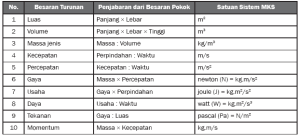
Besaran turunan adalah besaran  yang satuannya diturunkan dari besaran pokok. Jika suatu besaran turunan merupakan perkalian besaran pokok , satuan besaran turunan itu juga merupakan perkalian satuan besaran pokok, begitu juga berlaku didalam satuan besaran turunan yang merupakan pembagian besaran pokok. Besaran turunan mempunyai ciri khusus antara lain : diperoleh dari pengukuran langsung dan tidak langsung, mempunyai satuan lebih dari satu dan diturunkan dari besaran pokok.

Tabel Besaran Turunan

Satuan adalah sebagai pembanding dalam suatu pengukuran besaran. Setiap besaran mempunyai satuan masing-masing, tidak mungkin dalam 2 besaran yang berbeda mempunyai satuan yang sama. Apa bila ada dua besaran berbeda kemudian mempunyai satuan sama maka besaran itu pada hakekatnya adalah sama. Sebagai contoh Gaya (F) mempunyai satuan Newton dan Berat (w) mempunyai satuan Newton. Besaran ini kelihatannya berbeda tetapi sesungguhnya besaran ini sama yaitu besaran turunan gaya.
a. Satuan Baku
Satuan baku adalah satuan yang telah diakui dan disepakati pemakaiannya secara internasional tau disebut dengan satuan internasional (SI).
Contoh: meter, kilogram, dan detik.
Sistem satuan internasional dibagi menjadi dua, yaitu:
1. Sistem MKS (Meter Kilogram Sekon)
2. Sistem CGS (Centimeter Gram Second)
Tabel Satuan Baku

Besaran Pokok	Satuan MKS	Satuan CGS
Massa	kilogram (kg)	gram (g)
Panjang	meter (m)	centimeter (cm)
Waktu	sekon (s)	sekon (s)
Kuat Arus	ampere (A)	statampere (statA)
Suhu	kelvin (K)	kelvin (K)
Intensitas Cahaya	candela (Cd)	candela (Cd)
Jumlah Zat	kilomole (mol)	mol

b. Satuan Tidak Baku
Satuan tidak baku adalah satuan yang tidak diakui secara internasional dan hanya digunakan pada suatu wilayah tertentu.
Contoh: depa, hasta, kaki, lengan, tumbak, bata dan langkah.
ALAT UKUR
Alat Ukur adalah sesuatu yang digunakan untuk mengukur suatu besaran.
Berbagai macam alat ukur memiliki tingkat ketelitian tertentu. Hal ini bergantung pada skala terkecil alat ukur tersebut. Semakin kecil skala yang tertera pada alat ukur maka semakin tinggi ketelitian alat ukur tersebut. Beberapa contoh alat ukur sesuai dengan besarannya, yaitu:
a. Alat Ukur Panjang
1. Mistar (Penggaris)
Mistar adalah ala ukur panjang dengan ketelitian sampai 0,1 cm atau 1 mm. Pada pembacaan skala, kedudukan mata pengamat harus tegak lurus dengan skala mistar yang di baca.

Gambar Penggaris

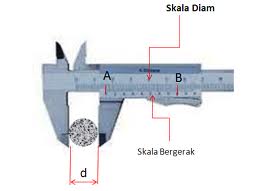
2. Jangka Sorong
Jangka sorong dipakai untuk mengukur suatu benda dengan panjang yang kurang dari 1mm. Skala terkecil atau tingkat ketelitian pengukurannya sampai dengan 0,01 cm atau 0,1 mm.
Umumnya, jangka sorong digunakan untuk mengukur panjang suatu benda, diameter bola, ebal uang logam, dan diameter bagian dalam tabung.
Jangka sorong memiliki dua skala pembacaan, yaitu:
a). Skala Utama/tetap, yang terdapat pada rahang tetap jangka sorong.
b). Skala Nonius, yaitu skala yang terdapat pada rahang sorong yang dapa bergeser/digerakan.

Gambar Jangka sorong

3. Mikrometer Sekrup
Mikrometer sekrup merupakan alat ukur panjang dengan ingkat ketelitian terkecil yaiu 0,01 mm atau 0,001 cm.
Skala terkecil (skala nonius) pada mikrometer sekrup terdapat pada rahang geser, sedangkan skala utama terdapat pada rahang tetap.
Mikrometer sekrup digunakan untuk mengukur diameter benda bundar dan plat yang sangat tipis.

Gambar Micrometer sekrup

b. Alat Ukur Massa
Alat ukur yang digunakan untuk mengukur massa suatu benda adalah neraca. Berdasarkan cara kerjanya dan keelitiannya neraca dibedakan menjadi tiga, yaitu:
1. Neraca digital, yaitu neraca yang bekerja dengan sistem elektronik. Tingkat ketelitiannya hingga 0,001g.

Gambar Neraca Digital

2. Neraca O’Hauss, yaitu neraca dengan tingkat ketelitian hingga 0.01 g.

Gambar Neraca O’hauss

3. Neraca sama lengan, yaitu neraca dengan tingkat ketelitian mencapai 1 mg atau 0,001 g.

Gambar Neraca Lengan

c. Alat Ukur Waktu
Satuan internasional untuk waktu adalah detik atau sekon. Satu sekon standar adalah waktu yang dibuuhkan oleh atom Cesium-133 untuk bergetar sebanyak 9.192.631.770 kali.
Alat yang digunakan untuk mengukur waktu, antara lain jam matahari, jam dinding, arloji (dengan ketelitian 1 sekon), dan stopwatch (ketelitian 0,1 sekon).

gambar Arloji

Gambar Stopwacth

Besaran berdasarkan arah dapat dibedakan menjadi 2 macam

1. Besaran vektor adalah besaran yang mempunyai nilai dan arah sebagai contoh besaran kecepatan, percepatan dan lain-lain.
2. Besaran sekalar adalah besaranyang mempunyai nilai saja sebagai contoh kelajuan, perlajuan dan lain-lain.

ANGKA PENTING
Angka Penting : Semua angka yang diperoleh dari hasil pengukuran dengan alat ukur, terdiri dari :
•    Angka pasti
•    Angka taksiran

Read More ->>

BESARAN SKALAR DAN VEKTOR

BESARAN SKALAR DAN VEKTOR

1.      Besaran Skalar 
Besaran Skalar adalah suatu besaran yang mempunyai besar saja.Contoh  :  panjang , massa , waktu , massa jenis , usaha , energi , daya .
Jumlah /selisih vektor adalah jumlah atau selisih vektor disebut resultan vektor 

2.      Besaran Vektor 
Besaran Vektor  adalah besaran yang mempunyai besar dan arah Contoh besaran vektor :  kecepatan , percepatan , gaya , berat , impuls , momentum.Vektor dapat digambar dengan sebuah tanda anak panah. 

  

Penjumlahan Vektor 
 1. Penjumlahan vektor dengan cara poligon

                     

contoh untuk penjumlahan 3 vektor

            
Penjumlahan vektor F1, vektor F2 dan vektor F3 tersebut di atas dengan  cara poligon gaya dan vektor F_R sebagai hasil penjumlahan dari ketiga vector tersebut. Dengan demikian secara penjumlahan vektor dapat dinyatakan:

 

 Penjumlahan empat buah vektor A, B, C dan D  secara grafis (metode poligon) V_R = A + B + C + D 

 Penjumlahan dengan metode poligon maka vektor resultan V_R adalah segmen garis berarah dari pangkal vektor A ke ujung vektor B yang menyatakan hasil penjumlahan vektor A dan B .         

                                         

3. Penjumlahan vektor dengan cara jajaran genjang  

                        

Penjumlahan dua buah vektor A dan B dengan metode jajar genjang yaitu dengan cara menyatukan pangkal kedua vektor A dan B , kemudian dari titik ujung vektor  A ditarik garis sejajar dengan vektor B dan juga dari titik ujung vektor A ditarik garis sejajar dengan vektor  B . Vektor resultan V_R diperoleh dengan menghubungkan titik pangkal ke titik perpotongan kedua garis sejajar tersebut di atas

Besar vektor resultan V_R yang ditunjukkan pada Gambar di atas dapat dicari dengan persamaan cosinus berikut ini:

Contoh Soal 

Dua buah vektor kecepatan A dan B sebidang berturut-turut besarnya 8 satuan dan 6 satuan, bertitik tangkap sama dan mengapit sudut 30^o Tentukan besar dan arah resultan  vektor tersebut tersebut! 

 

                                      VR=8²+6²+2.6.8.cos 30^o
                                      VR=64+36+96.0,5√3
                                      VR = 100 + 48√3

                                      VR = 100 + 48 (1,73)

                                      VR = 100 + 83,04

                                      VR = 183,04 m/s
catatan:
cos  30^o = 1/2√3 dapat dilihat ditabel di bawah ini.   
Tabel sin, cos dan tan

Read More ->>

Jarak, Perpindahan,Kecepatan, Kelajuan dan Percepatan

Jarak dan Perpindahan

Jarak adalah panjang lintasan yang ditempuh benda tanpa memerhatikan arahnya. Jarak merupakan besaran skalar.

Perpindahan adalah perubahan posisi benda ditinjau dari posisi awal dan posisi akhir benda tersebut.

Perpindahan merupakan besaran vektor, sehingga dapat bernilai positif maupun negatif. Lihat gambar berikut ini!

Gerak satu dimensi

Pada gerak satu dimensi seperti pada gambar di atas, perpindahan bernilai positif jika arahnya ke kanan dan negatif jika arahnya ke kiri. Jika benda bergerak dari posisi x1 ke posisi x2, perpindahannya (∆x) dapat dituliskan sebagai:

Gerak dua dimensi

Pada gerak dua dimensi seperti gambar di samping, perpindahan dapat dicari menggunakan perhitungan resultan dari AB dan BC. Sehingga cara mencarinya menggunakan dalil pythagoras berikut ini:

dengan arah:

Kecepatan dan Kelajuan

Kelajuan sebuah benda yang bergerak menyatakan jarak yang ditempuh benda tersebut tiap satuan waktu tanpa memerhatikan ke arah mana benda tersebut bergerak. Maka dapat disimpulkan bahwa kelajuan merupakan besaran skalar. 

Kecepatan menyatakan perpindahan benda tiap satuan waktu dengan memerhatikan arahnya. Maka dapat disimpulkan bahwa kecepatan merupakan besaran vektor.

Kecepatan dan Kelajuan Rata-Rata

Setelah mengerti bahwa kecepatan dan kelajuan mengandung makna yang berbeda dan dengan mengingat perbedaan antara konsep jarak dan perpindahan, maka berikut ini akan dijelaskan mengenai kelajuan rata-rata dan kecepatan rata-rata.

Kelajuan rata-rata didefinisikan sebagai perbandingan jarak yang ditempuh terhadap waktu yang diperlukan untuk menempuh jarak tersebut.

Kecepatan rata-rata didefinisikan sebagai perbandingan perpindahan yang terjadi terhadap waktu yang diperlukan untuk melakukan perpindahan tersebut.

Kecepatan dan Kelajuan Sesaat

Kecepatan rata-rata maupun kelajuan rata-rata pada pembahasan sebelumnya tidak menjelaskan secara rinci tentang gerakan benda. Dalam banyak hal, informasi yang dibutuhkan adalah kecepatan benda itu pada saat tertentu di posisi tertentu, bukan selama selang waktu tertentu. Kecepatan itu disebut dengan kecepatan sesaat yang dapat diperoleh dengan mengambil selang waktu ∆t yang sangat kecil, mendekati nol. 

Kecepatan sesaat secara matematis dapat dituliskan sebagai berikut.

Umumnya, konsep kecepatan sesaat digunakan pada kejadian yang membutuhkan waktu yang sangat pendek. Dalam kehidupan sehari-hari kecepatan sesaat disebut dengan kecepatan saja tanpa kata sesaat.

Selain itu ada pula istilah kelajuan sesaat yang merupakan besar (harga mutlak) dari kecepatan sesaat. Nilainya selalu positif dan merupakan besaran skalar. Misalnya, kelajuan yang tertera pada speedometer.

Percepatan

Seringkali benda-benda tidak bergerak kecepatan konstan. Sebuah benda dikatakan bergerak dengan percepatan atau perlambatan. Perlambatan adalah nama lain dari percepatan negatif.

Ketika sebuah mobil berangkat dari keadaan diam meninggalkan suatu tempat misalnya, mobil bergerak dipercepat. Namun, ketika mobil tersebut akan tiba di tujuannya, maka mobil tersebut akan mengurangi kecepatannya atau bergerak diperlambat hingga pada akhirnya berhenti bergerak. Jadi, percepatan atau perlambatan itu ada jika kecepatan benda berubah.

Selain percepatan ada pula istilah perlajuan. Perlajuan merupakan besar (harga mutlak) dari percepatan atau perlambatan. Nilainya selalu positif dan merupakan besaran skalar.

Percepatan Rata-Rata

Percepatan rata-rata didefinisikan sebagai perbandingan perubahan kecepatan dengan selang waktunya. Secara matematis ditulis sebagai berikut:

Percepatan rata-rata negatif artinya sama dengan perlambatan rata-rata.

Percepatan Sesaat

Percepatan rata-rata tidak menggambarkan percepatan pada suatu waktu tertentu. Percepatan pada waktu tertentu disebut dengan percepatan sesaat atau dalam kehidupan sehari-hari hanya disebut percepatan.

Percepatan sesaat didefinisikan sebagai limit percepatan rata-rata ketika selang waktunya mendekati nol (sangat kecil). Secara matematis ditulis sebagai berikut:

Kecepatan dan Kelajuan Jarak dan Perpindahan Percepatan

Read More ->>

Gerak Lurus Beraturan (GLB) dan Gerak Lurus Berubah Beraturan (GLB)

Gerak Lurus Beraturan (GLB)

Gerak lurus beraturan (GLB) adalah gerak suatu benda yang menempuh lintasan lurus yang dalam waktu sama benda menempuh jarak yang sama. Gerak lurus beraturan (GLB) juga dapat didefinisikan sebagai gerak suatu benda yang menempuh lintasan lurus dengan kelajuan tetap.
Dalam kehidupan sehari-hari, jarang ditemui contoh benda yang bergerak lurus dengan kecepatan tetap. Misalnya, sebuah mobil yang bergerak dengan kelajuan 80 km/jam, kadang-kadang harus memperlambat kendaraannya ketika ada kendaraan lain di depannya atau bahkan dipercepat untuk mendahuluinya.
Gerak lurus kereta api dan gerak mobil di jalan tol yang bergerak secara stabil bisa dianggap sebagai contoh  gerak lurus dalam keseharian.

Untuk lebih jelasnya lihat gambar berikut.

Kedudukan sebuah mobil yang sedang bergerak lurus beraturan

Dari gambar di atas, tampak bahwa setiap perubahan 1 sekon, mobil tersebut menempuh jarak yang sama, yaitu 10 m.
Dengan kata lain mobil tersebut mempunyai kecepatan yang sama, yaitu 10 m/s.

Grafik jarak terhadap waktu untuk gerak lurus beraturan
Sebuah mobil bergerak lurus dengan kecepatan tetap yaitu 10 m/s dapat ditunjukkan dengan tabel dan grafik sebagai berikut.

Tabel hubungan waktu dan jarak pada GLB

grafik hubungan waktu dan jarak pada GLB

Pada gerak luru beraturan, berlaku persamaan :

dengan
v = kecepatan (m/s)
s = perpindahan (m)
t = waktu yang diperlukan (s)
Dari persamaan itu, dapat dicari posisi suatu benda yang dirumuskan dengan :
s = v.t

Contoh soal GLB
Sebuah mobil bergerak di sebuah jalan tol. Pada jarak 5 kilometer dari pintu gerbang tol, mobil bergerak dengan kelajuan tetap 90 km/jam  selama 20 menit. Tentukan :
a. jarak yang ditempuh mobil selama 20 menit
b. posisi mobil dari gerbang jalan tol

Penyelesaian
jarak mula-mula s0 = 5 km
kecepatan (v) = 90 km/jam
waktu (t) = 20 menit = 1/3 jam

a. jarak yang ditempuh mobil selama 20 menit
s = v. t = (90 km/jam).(1/3 jam) = 30 km

b. posisi mobil dari gerbang jalan tol
s = s0 + v.t = 5 + 30 = 30 km

Pengertian Gerak Lurus Berubah Beraturan (GLBB)

Pengertian GLBB sangatlah beragam. Tergantung sumber dan pemikiran masing-masing orang. Berikut adalah beberapa pengertian GLBB menurut beberapa sumber:

• Gerak lurus berubah beraturan (GLBB) adalah gerak lurus suatu obyek, di mana kecepatannya berubah terhadap waktu akibat adanya percepatan yang tetap. Akibat adanya percepatan rumus jarak yang ditempuh tidak lagi linier melainkan kuadratik (sumber: id.wikipedia.org).
• Gerak Lurus Berubah Beraturan (GLBB) adalah gerak lurus pada arah mendatar dengan kecepatan v yang berubah setiap saat karena adanya percepatan yang tetap. Dengan kata lain benda yang melakukan gerak dari keadaan diam atau mulai dengan kecepatan awal akan berubah kecepatannya karena ada percepatan (a= +) atau perlambatan (a= –) (sumber: bebas.xlsm.org).
• GLBB adalah gerak suatu benda pada lintasan garis lurus dengan percepatan tetap. Maksud dari percepatan tetap yaitu percepatan percepatan yang besar dan arahnya tetap (sumber: sidikpurnomo.net).

Jadi, gerak lurus berubah beraturan adalah gerak benda dengan lintasan garis lurus dan memiliki kecepatan setiap saat berubah dengan teratur.

Pada gerak lurus berubah beraturan gerak benda dapat mengalami percepatan atau perlambatan. Gerak benda yang mengalami percepatan disebut gerak lurus berubah beraturan dipercepat, sedangkan gerak yang mengalami perlambatan disebut gerak lurus berubah beraturan diperlambat.
Benda yang bergerak semakin lama semakin cepat dikatakan benda tersebut mengalami percepatan.
Suatu benda melakukan gerak lurus berubah beraturan (GLBB) jika percepatannya selalu konstan. Percepatan merupakan besaran vektor (besaran yang mempunyai besar dan arah). Percepatan konstan berarti besar dan arah percepatan selalu konstan setiap saat. Walaupun besar percepatan suatu benda selalu konstan tetapi jika arah percepatan selalu berubah maka percepatan benda tidak konstan. Demikian juga sebaliknya jika arah percepatan suatu benda selalu konstan tetapi besar percepatan selalu berubah maka percepatan benda tidak konstan.
Karena arah percepatan benda selalu konstan maka benda pasti bergerak pada lintasan lurus. Arah percepatan konstan = arah kecepatan konstan = arah gerakan benda konstan = arah gerakan benda tidak berubah = benda bergerak lurus.Besar percepatan konstan bisa berarti kelajuan bertambah secara konstan atau kelajuan berkurang secara konstan. Ketika kelajuan benda berkurang secara konstan, kadang kita menyebutnya sebagai perlambatan konstan. Untuk gerakan satu dimensi (gerakan pada lintasan lurus), kata percepatan digunakan ketika arah kecepatan = arah percepatan, sedangkan kata perlambatan digunakan ketika arah kecepatan dan percepatan berlawanan.
Grafik kecepatan terhadap waktunya adalah seperti gambar di bawah ini.

Grafik menunjukkan gerak lurus berubah beraturan karena garis pada grafik lurus yang menunjukkan bahwa percepatannya tetap.

Rumus Gerak Lurus Berubah Beraturan (GLBB)

Rumus GLBB ada 3, yaitu:

Keterangan:

Vt = kecepatan akhir atau kecepatan setelah t sekon (m/s)

V0 = kecepatan awal (m/s)

a = percepatan (m/s2)

t = selang waktu (s)

s = jarak tempuh (m)

Hubungan GLBB dengan Matematika

Kita bisa menghitung jarak tempuh yang dialami benda yang bergerak lurus berubah beraturan dengan rumus luas matematika. Seperti pada contoh gambar dibawah ini:

Sebuah titik partikel melakukan gerak dengan grafik hubungan kecepatan (v) terhadap
waktu (t) seperti terlihat pada gambar di samping. Berapakah jarak yang ditempuh titik partikel selama 8 sekon tersebut?

 

Jawab:

Cara Saya:
s = luas I + luas II + luas III
s = (¹⁄₂ . 4 . 10) + (2 . 10) + (¹⁄₂ . 2 . 10)
s = 20 + 20 + 10 = 50 m
Nah, jauh lebih simple dan cepat, kan? :)

Contoh GLBB

Gerak Jatuh Bebas

Gerak jatuh bebas adalah gerak benda yang jatuh dari suatu ketinggian tanpa kecepatan awal di sekitar bumi. Gerak jatuh bebas dipengaruhi oleh gaya gravitasi. Benda-benda yang jatuh bebas. Rumus ini akurat saat benda dijatuhkan di ruang hampa.

Keterangan:

vt = kecepatan saat t sekon (m/s)

g = percepatan gravitasi bumi (9,8 m/s2)

h = jarak yang ditempuh benda (m)

t = selang waktu (s)

Gerak Vertikal ke Bawah

Gerak Vertikal ke bawah adalah gerak suatu benda yang dilemparkan vertikal ke bawah dengan kecepatan awal dan dipengaruhi oleh percepatan. Rumus-rumus gerak vertikal ke bawah adalah sebagai berikut.

Keterangan:

h = jarak/perpindahan (m)

v0 = kecepatan awal (m/s)

vt = kecepatan setelah t (m/s)

g = percepatan gravitasi (9,8 m/s2)

t = selang waktu (s)

Gerak Vertikal ke Atas

Gerak vertikal ke atas adalah gerak suatu benda yang dilempar vertikal ke atas dengan kecepatan awal tertentu (v₀) dan percepatan g saat kembali turun. Rumus gerak vertikal ke atas adalah sebagai berikut.



Di titik tertinggi benda, kecepatan benda adalah nol. Persamaan yang berlaku di titik tertinggi adalah sebagai berikut.

Keterangan:

tnaik = selang waktu dari titik pelemparn hingga mencapai titik tertinggi (s)

v0 = kecepatan awal (m/s)

g = percepatan gravitasi (9,8 m/s2)

hmaks = jarak yang ditempuh hingga titik tertinggi (m)

Saat mulai turun, persamaannya sama seperti gerak jatuh bebas. Rumusnya adalah:

Jadi, dapat disimpulkan bahwa waktu saat naik sama dengan waktu saat turun.

Read More ->>

Gerak Jatuh Bebas dan Gerak Vertikal

Gerak Jatuh Bebas

Gerak jatuh bebas adalah gerak yang dijatuhkan tanpa kecepatan awal. Jika gaya hambatan udara diabaikan, maka gaya yang bekerja pada benda tersebut hanyalah gaya gravitasi (gaya berat benda). Benda tersebut akan mengalami gerak jatuh bebas dengan percepatan ke bawah sama dengan percepatan gravitasi.

Gerak Jatuh Bebas

Gerak jatuh bebas adalah gerak jatuh yang hanya dipengaruhi oleh gaya tarik bumi dan bebas dari hambatan gaya-gaya lain. Gerak jatuh bebas termasuk GLBB dipercepat dengan kecepatan awal V_o = nol dan percepatan sebesar percepatan gravitasi (g).

Aplikasi nyata dari gerak lurus berubah beraturan dengan percepatan a positif (gerak lurus dipercepat dengan percepatan a tetap) ini adalah suatu benda yang dijatuhkan dari ketinggian h meter dengan kecepatan awal nol atau tanpa kecepatan awal. Percepatan yang dialami oleh benda tersebut adalah percepatan gravitasi bumi g (m/s²). Lintasan gerak benda ini berupa garis lurus. Gerak benda semacam ini yang disebut gerak jatuh bebas.

Gerak jatuh bebas didefinisikan sebagai gerak suatu benda yang dijatuhkan dari ketinggian tertentu di atas tanah tanpa kecepatan awal dan dalam geraknya hanya dipengaruhi oleh gaya gravitasi.

Suatu benda dilepaskan dari ketinggian h meter di atas permukaan tanah tanpa kecepatan awal. Kecepatan pada saat t dapat dihitung dari persamaan berikut :

v_t = v₀ + at

Karena v₀ = 0 dan percepatan gravitasi a = g, maka kecepatan benda pada saat t adalah :

v_t = 0 + gt = gt

dengan :

v_t = kecepatan pada waktu t (m/s),
v₀ = kecepatan awal (t = 0) (m/s),
g = percepatan gravitasi bumi (m/s²),
t = waktu (s).

Ketinggian yang dicapai oleh benda h adalah analog dengan persamaan dengan s_t adalah h, dan v_o = 0,

Waktu yang diperlukan oleh benda untuk mencapai tanah dari ketinggian h dengan persamaan

Kecepatan benda pada saat t dapat diperoleh dengan memasukkan persamaan t dari persamaan berikut.

dengan:

v_t = kecepatan pada waktu t (m/s),
g = percepatan gravitasi bumi (m/s²),
h = ketinggian benda (m).

Contoh Soal Gerak Jatuh Bebas

Sebuah benda dijatuhkan dari ketinggian h = 20 m di atas permukaan tanah tanpa kecepatan awal. Gerak benda hanya dipengaruhi oleh gaya gravitasi (gaya tarik-menarik bumi) sehingga benda bergerak dengan percepatan sama dengan percepatan gravitasi bumi g = 10 m/s2. Berapa kecepatan benda saat mencapai tanah dalam m/s?

Penyelesaian:
Kecepatan benda v dapat dihitung menggunakan persamaan gerak jatuh bebas diatas yaitu:

v_t = v₀ + at = gt = 10 (m/s²) x t(s).

Waktu yang diperlukan t dapat dicari dengan menggunakan persamaan 

dengan :

h = 20 m,
g = 10 m/s².

Waktu yang diperlukan : 
Kecepatan benda saat mencapai tanah : v = gt = 10 m/s² x 2(s) = 20 m/s.

 Gerak Vertikal

Pengertian GerakVertikal ke Atas (GVA) – Gerak Vertikal ke Atas (GVA) adalah/ Gerak Vertikal ke Atas (GVA) yaitu/ Gerak Vertikal ke Atas (GVA) merupakan/ yang dimaksud Gerak Vertikal ke Atas (GVA)/ arti Gerak Vertikal ke Atas (GVA)/ definisi Gerak Vertikal ke Atas (GVA).

GerakVertikal ke Atas (GVA) adalah gerak benda yang dilempar ke atas dengan kecepatan awal (V₀) dan gesekan udara diabaikan merupakan geraklurus berubah beraturan (GLBB) yang mengalami perambatan. Percepatan yang dialami benda adalah a= -g.

Persamaan pada gerak vertical ke atas diperoleh dari persamaan gerak lurus berubah beraturan:

V_t = V₀ – gt

H = V₀t – ½ gt²

V_t² = V₀² – 2gh

Pada saat mencapai tinggi maksumum, kecepatan benda sama dengan nol (V_t = 0). Waktu untuk mencapai tinggi maksimum (t_m) dirumuskan sebagai berikut:

t_m = V₀ / g

Tinggi maksimum (h_m) dirumuskan sebagai berikut:

H_m = V₀² / 2g

Read More ->>